By Paul Heller (DPhil Student at the Uehiro Oxford Institute)
On Friday 16th June, Jacob Nebel, Professor of Philosophy at Princeton University, gave the 2025 Parfit Memorial Lecture. Professor Nebel’s lecture was entitled: “The Procreation Asymmetry: Some Puzzles.” This year’s lecture was jointly hosted by the Uehiro Oxford Institute and the Global Priorities Institute at Pembroke College.
Nebel began by introducing the ‘procreation asymmetry’ with a quote from Derek Parfit, to whose memory the lecture was dedicated. Parfit wrote that “most of us … think that there is nothing wrong with not having children, even if they would be very happy. But we think that having children who are bound to suffer is wrong.”
Nebel made two clarifications about how he would understand the asymmetry. First, this asymmetry has its source not only in facts about what human procreation is like. Though those facts are relevant to our duties (that is, to when we act wrongly), the asymmetry persists even if we abstract away from them. For instance, the asymmetry entails that it would not be wrong to refrain from pressing a button which would magically create new, and happy, lives on a distant planet. Second, Nebel understands the asymmetry only as an asymmetry in our moral obligations, not about which states of affairs would be good or bad. Citing John Broome’s influential discussion, he rejects any corresponding asymmetry in relation to what is good – it would indeed be better if there were more happy lives, and worse if there were more suffering filled lives. In the jargon, Nebel presented the procreation asymmetry as an asymmetry in rightness, but not an asymmetry in goodness.
Nebel’s goal then was to chart a course on which we reject any asymmetry in goodness, but accept an asymmetry in rightness, with regard to creating new people. Some might think this is an immediate non-starter: other things being equal, we always have a reason to make things go better. So, if I refused to press the person-creating button even though it would cost me and others nothing, I would be costlessly refusing to act on a moral reason which I have. Surely such a refusal would be wrong.
We can respond to this worry by distinguishing between what we ought to do, and what we are morally required to do. We find everyday appeal to this distinction in phrases like “employees must wash hands but really everybody should.” Perhaps, then, creating happy people is something like non-employee hand washing – though we do have a reason to do it, and costless refusal is a failure to act on a reason we have, we are not required to do it.
The ought/must distinction seems promising, but there is a problem. Defenders of the procreation asymmetry must also face up to the fact that reasonable ways of capturing the asymmetry conflict with other plausible principles about what we are morally required to do. This brings us to another point of Parfit’s work, the ‘Mere Addition Paradox’. Perhaps, then, we can learn something about how to square the rightness asymmetry with a goodness symmetry by looking at how the defender of the asymmetry should respond to this paradox.
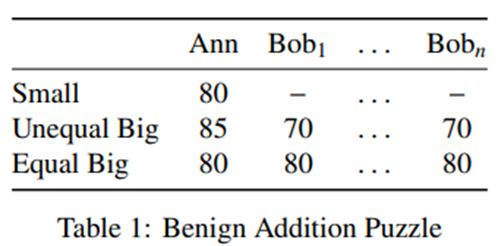
Nebel then took the audience through a series of such puzzles, showing how the procreation asymmetry might conflict with other principles about what is and is not permissible. Perhaps most important was his second puzzle, which we can understand using the following table:
This table represents an imaginary choice scenario in which we have three options “Small”, “Unequal Big” and “Equal Big.” Ann and the Bobs are imaginary people (relation to the builder unclear). Depending on which option we choose, Ann and perhaps some number of Bobs will live. If a person would live following our choice, their overall quality of life is entered as a number. If they would not live following our choice, a dash is entered instead. It’s important to emphasise here that “not living following our choice” is not dying – if we choose Small, no Bobs will get hurt, they just will never exist in the first place.
From this choice situation we can derive a contradiction between the procreation asymmetry and plausible seeming principles. The foregoing provides a brief overview of Nebel’s argument, but interested listeners should see sections 27:13-31:50 of the recording for a brilliant explanation of the problem this choice situation presents.
We start by noting that it should be impermissible (that is wrong) to choose Unequal Big when Equal Big is an option. As compared to Unequal Big, Equal Big involves the Bobs, who are more numerous than Ann, all gaining more than Ann loses and is better from the point of view of equality. More generally, we can say that when option is worse for more people, worse by more for those people, and worse from the point of view of equality than some other option, that option is impermissible to choose. This principle is known as “Not-Elitism” – it would be “elitist” to put such a priority on how Ann, the best-off person, is doing.
Then, we move from the wrongness of choosing Unequal Big to the Wrongness of Small. The “Benign Addition” principle says that if something like Small is a permissible option, then it should also be acceptable to choose an option in which all of the population of Small is better off, and new people are added who have happy lives. Compare Unequal Big to Small: Ann, who will exist regardless, is better off, and all the Bobs get to live happy lives rather than not live. What objection could there possibly be to choosing Unequal Big over Small? So, given that Small’s permissibility should imply Unequal Big’s permissibility, we are licensed to reason from Unequal Big’s impermissibility to Small’s impermissibility. Put another way, since Unequal Big is wrong to choose, and since Unequal Big is a straightforward improvement over Small, Small must also be wrong to choose.
If Unequal Big and Small are both impermissible, then Equal Big is our only permissible option. But notice how Equal Big Relates to Small – Equal Big is just Small, plus a lot of extra people. This seems to contradict the procreation asymmetry! By being required to choose Equal Big over Small, we are being morally required to create new happy people. So, in the right circumstances, it seems it could indeed be wrong to refuse to press the person-creating button.
After exploring some variants of the puzzle which reveal the depth of the issue, Nebel turned to his own solution. The basic idea behind his solution is that “wrongs require victims,” or more specifically, an act can only be wrong if there is somebody who it wrongs. Fleshing out this idea requires some careful consideration of what counts as a wronging, but Nebel suggests the following as a good starting point: (1) A person is wronged when they are made worse off than they would have been under some option which is overall better, but (2) a person is not wronged if the only way to make them better off would wrong somebody else, not wronged in the original choice.
Nebel’s suggestion may sound complex at first, but we can understand it by applying it one step at a time to the table above. Let’s assume for simplicity that we measure overall goodness just by taking the sum of how well off everybody is under a certain option (the sum of the numbers on the rows of our table). Invoking (1), it would initially appear that Ann would be wronged by our choosing Small, since Unequal Big would make her better off and would be overall better. But notice that Unequal Big introduces all the Bobs. These Bobs can now legitimately complain that they were wronged by Unequal Big, since they would have been Better off under Equal Big and Equal Big would have been better. We can therefore use (2) to block Ann’s complaint: Ann is not wronged because the only way to make her better off would wrong the Bobs.
Using Nebel’s suggestion, we can now argue that it was our move from the impermissibility of Unequal Big to the impermissibility of Small that caused problems. For an act to be impermissible (flat out wrong) requires for it to wrong somebody. Unequal Big is wrong because it wrongs the Bobs. But Small does not wrong the Bobs, because under Small there are no Bobs to be wronged. And small does not wrong Ann, for the reasons described above. The problem, then, was with the “Benign Addition” principle. Rejecting the Benign Addition principle and using Nebel’s account of wronging, we can vindicate the claim that both Small and Equal Big are permissible.
Nebel’s lecture was followed by a lively Q&A, which included both an able defence of his view and the welcome surprise of some bonus slides. Nebel also took a moment to consider Derek Parfit, with whom he worked during his Oxford BPhil, recording both his personal debt to Parfit and the enormous value of his academic work.
A recording of the lecture can be accessed here: https://youtu.be/7FIxGvDuaNM